18.03.2019 Geräuschlose Dichtungen bevorzugt
Das Prandtl-Tomlinson-Reibungs-Modell als Erklärungsversuch von Geräuschentwicklungen an Gleitringdichtungen – Teil 2: Das Modell
Geräusche, verursacht durch Dichtungen, kommen nicht allzu häufig vor. Wenn Dichtungen in der Praxis „quietschen“, ist die Lösung dieses Problems oft mit erheblichem Aufwand verbunden. Besser man berücksichtigt dies vorher.
Prandtl-Tomlinson-Modell
Grundlage des Prandtl-Tomlinson-Modells [1] für Reibungsmechanismen auf atomarer Skala ist eine resultierende periodische Anregung. Das Modell beschreibt eindimensional viele wesentliche Eigenschaften der trockenen Reibung:
• Zur Bewegung muss eine bestimmte Mindestkraft aufgebracht werden (Haften).
• Die Gleitreibung ist aufgrund der Kontinuität kleiner als die Haftreibung.
• Wird die Kraft während der Bewegung reduziert, so bewegt sich der Körper trotzdem aufgrund seiner Massenträgheit weiter.
• Der Körper kommt infolge der „Reibung“ (Eigendämpfung b des Systems) zum Stillstand.
Prandtl [2] betrachtete eine eindimensionale Bewegung eines Massenpunktes m (für Gleitringdichtungen die Masse des Gleit- und/oder Gegenrings) nach Bild 2 in einem periodischen Potenzial mit einer Wellenzahl k (Periode) und einer geschwindigkeitsproportionalen Dämpfung b unter Einwirkung von N im Sinne einer Kraft. Mit einer Umfangs-Laufkoordinate x, der Masse m sowie N ergibt sich für die Differenzialgleichung 2. Ordnung:
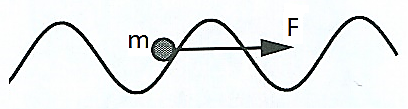
Bild 1: Prandtl-Tomlinson-Modell eines Massenpunktes in einem periodischen Potenzial (Bild: HAW München)
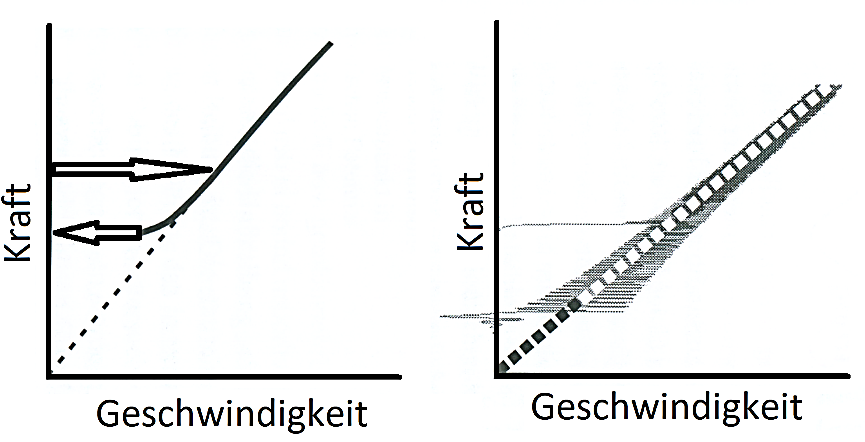
Bild 2: Makroskopisches Reibungsgesetz mit geschwindigkeitsproportionaler Reibung (links) sowie Prandtl-Tomlinson-Modell mit zeitlich linearer Steigung der Kraft (rechts) (Bild: HAW München)

